難易度・正答率・重要度
- 難易度: ★★☆☆☆(二資産ポートフォリオと相関)
- 正答率: ★★★★☆(定義の理解で解ける)
- 重要度: ★★★☆☆(分散効果の本質)
問題文
次の文章は、X、Yの2資産から構成されるポートフォリオのリターンとリスクの変化について、説明したものである。空欄A~Dに入る語句の組み合わせとして、最も適切なものを下記の解答群から選べ。
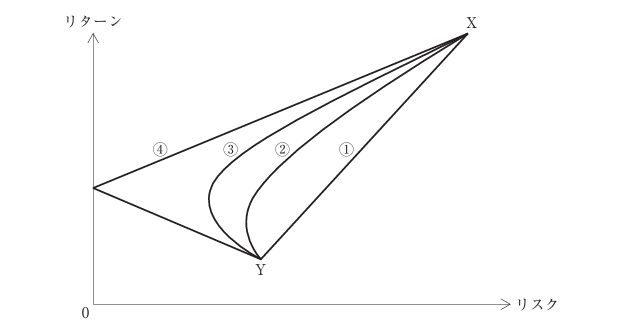
以下の図は、X、Yの2資産から構成されるポートフォリオについて、投資比率をさまざまに変化させた場合のポートフォリオのリターンとリスクが描く軌跡を、2資産間のAが異なる4つの値について求めたものである。
X、YのAがBのとき、ポートフォリオのリターンとリスクの軌跡は①に示されるように直線となる。AがCなるにつれて、②、③のようにポートフォリオのリスクをより小さくすることが可能となる。
AがDのとき、ポートフォリオのリスクをゼロにすることが可能となり、④のような軌跡を描く。
〔解答群〕
ア
A:相関係数 B:-1 C:大きく D:ゼロ
イ
A:相関係数 B:+1 C:小さく D:-1
ウ
A:ベータ値 B:ゼロ C:大きく D:+1
エ
A:ベータ値 B:+1 C:小さく D:-1
出典:中小企業診断協会|2019年度 第1次試験問題|財務・会計(PDF)
解答
- 正解:イ(A:相関係数、B:+1、C:小さく、D:-1)
解説
- A:相関係数
二資産の組合せで軌跡の形を決めるのは相関係数。ベータ値は市場に対する相対感度であり、二資産間の組合せの形状とは関係しない。 - B:+1(完全正の相関)
相関が+1のとき、二資産の組合せは直線上に並び、分散効果は生じない。問題文の「①は直線」に一致。 - C:小さく
相関係数が+1から0、負へと「小さく」なるほど分散効果が高まり、同じ期待リターンでリスクをより低くでき、軌跡は②、③のように外側から内側(左側)へ膨らむ。 - D:-1(完全負の相関)
相関が-1のとき、適切な比率で組み合わせればリスク(標準偏差)をゼロにできる。④の軌跡の説明に一致。
学習のポイント
- 分散効果は「相関が低いほど強い」。完全正の相関では効果ゼロ、完全負の相関では理論上リスクゼロが可能。
- 二資産の組合せ軌跡は、相関+1で直線、-1で折れ線的にゼロリスク点を持ち、それ以外では内側へ湾曲する。
- ベータ(SML)と相関(CML/効率的フロンティアの形状)は別の概念。混同しないこと。
