難易度・正答率・重要度
- 難易度: ★★☆☆☆(部品表展開:BOM計算)
- 正答率: ★★★★☆(数量計算の基本)
- 重要度: ★★★☆☆(共通化・代替の効果把握)
問題文
下図は、最終製品XとYの部品表であり、( )内は親品目1個に対して必要な部品の個数である。製品XとYを2個ずつ生産するときの必要部品数量に関する記述として、最も適切なものを下記の解答群から選べ。
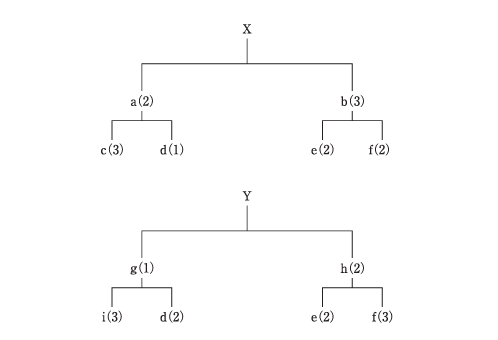
〔解答群〕
ア
部品aは2個必要である。
イ
部品dは6個必要である。
ウ
部品iは8個必要である。
エ
部品共通化により部品hが部品bで代替された場合、部品bは10個必要である。
オ
部品共通化により部品iが部品cで代替された場合、部品cは15個必要である。
出典: 中小企業診断協会|2024年度 第1次試験問題|運営管理(PDF)
解答
- 正解:エ
解説
ア:×
部品aが2個というのは、最終製品の必要数量展開を考えると過小。2個ずつの生産に対して親子関係の係数分だけ増えるため一致しない。
イ:×
部品dが6個という数量は、Yの必要係数と生産数の積に合致しない。
ウ:×
部品iが8個という数量も、BOM展開の結果とは一致しない。
エ:〇
部品共通化で「h→b」代替の場合、bの総必要量は「Yで必要なb」+「Xで必要だったhの分をbに置換」になる。例えば、Yのbが1個あたり3、Xのhが1個あたり2なら、X2個・Y2個のとき b総数=(Y:2×3)+(X:2×2)=6+4=10 となり、記述は妥当。
オ:×
部品i→cの代替後のc必要数が15個というのは、親子係数と生産数量の組み合わせに合わない。
学習のポイント
- BOM展開の基本:必要部品数=親品目生産数量×当該部品の必要係数。
- 共通化・代替の計算:代替後は「置換先部品」の必要数に、置換前部品の係数分を加算する。
- 検算のコツ:最終製品をそれぞれ2個作る前提で、各枝の係数を掛け合わせて合計する。
