過去問解説(運営管理)_2021年(令和3年) 第4問

難易度・正答率・重要度

• 難易度: ★★★☆☆（直交配列と交互作用の理解）
• 正答率: ★★☆☆☆（線点図の読み取り力が問われる）
• 重要度: ★★★☆☆（実験計画法の基礎）

---

問題文

以下の文章を読んで、下記の設問に答えよ。

ある工作機械において、現行の加工条件よりさらに良い条件を探すため、2水準系のL8直交配列表を用いた実験を計画することとなった。調べたい因子および交互作用は、以下のとおりである。

• 因子：Ａ、Ｂ、Ｃ、Ｄ
• 交互作用：Ａ#Ｂ、Ａ#Ｃ

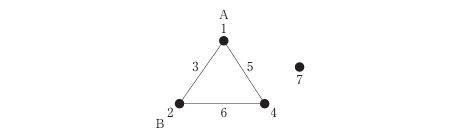
（設問1）

以下の標準的な線点図を用いて、因子Ａを1列目、因子Ｂを2列目に割り付けるとき、3列目～7列目に割り付く因子、交互作用、誤差の組み合わせとして、最も適切なものを下記の解答群から選べ。

設問2

実験の結果を分散分析し、下表を得た。平均平方および分散比を計算して検定をした結果、有意水準5％（下表右参照）で有意となる要因の数として、最も適切なものを下記の解答群から選べ。なお、分散比計算後、プーリングは行わないこととする。

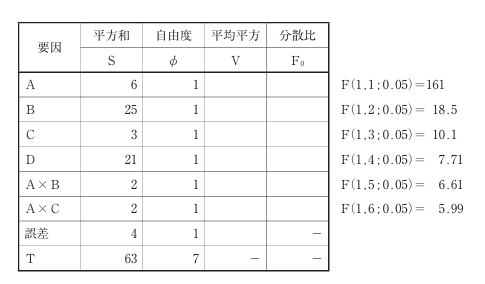
〔解答群〕

出典： 中小企業診断協会｜2021年度 第1次試験問題｜運営管理（PDF）

解答

• 設問1：ア
• 設問２：ア

---

解説 (設問1)

• L8直交配列表は、2水準の因子を最大7列まで割り付け可能な実験計画法の代表的な配列。
• 線点図を用いて交互作用の割り付けを行う際、交互作用列は対応する因子列の論理積（XOR）で決定される。
• 例：A#B → 列1と列2のXOR → 列3
• A#C → 列1と列4のXOR → 列5
• 残りの列には因子C、D、誤差を割り付ける。誤差は交互作用以外の未使用列に割り当てるのが一般的。

---

解説 (設問2)

• 各要因の分散比（F値）は「平均平方 ÷ 誤差の平均平方」で求める。誤差の平方和＝4、自由度＝1 → 平均平方＝4。
• 各要因のF値は以下の通り：
  A：6 ÷ 4 = 1.5（F(1,1;0.05)=161 → 有意でない）
  B：25 ÷ 4 = 6.25（F(1,2;0.05)=18.5 → 有意でない）C：3 ÷ 4 = 0.75（F(1,3;0.05)=10.1 → 有意でない）D：21 ÷ 4 = 5.25（F(1,4;0.05)=7.71 → 有意でない）A#B：2 ÷ 4 = 0.5（F(1,5;0.05)=6.61 → 有意でない）A#C：2 ÷ 4 = 0.5（F(1,6;0.05)=5.99 → 有意でない）
• すべての要因でF値が有意水準の閾値を下回っており、有意な要因は存在しない。

学習のポイント

• 交互作用の割り付け：交互作用列は因子列の論理積で決定。線点図を活用して正確に割り付ける。
• L8直交配列の構造：7列に因子・交互作用・誤差を割り付ける。因子数と交互作用数に応じて列を選定。
• 誤差の扱い：誤差は交互作用に割り付けない列に配置し、分散分析の残差として活用される。
• 実験計画法の目的：少ない試行で因子の影響を効率的に分析するための手法。品質管理や工程改善に有効。
• 分散分析（ANOVA）：要因の影響を検定するために、分散比（F値）を用いる。
• F値の計算：平均平方 ÷ 誤差平均平方。誤差の自由度と平方和から誤差平均平方を算出。
• 有意水準とF分布：自由度に応じたF分布の臨界値と比較して、有意かどうかを判断。
• プーリングなしの検定：誤差項を固定し、交互作用や主効果を個別に評価する。