難易度・正答率・重要度
- 難易度: ★★★★☆(線形計画法と制約緩和の理解)
- 正答率: ★★☆☆☆(グラフと利益関数の読み取り力が問われる)
- 重要度: ★★★☆☆(資源配分と利益最大化の応用)
問題文
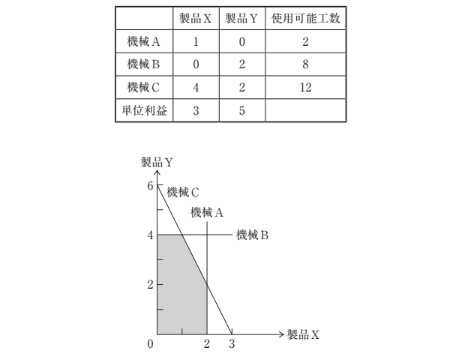
ある工場では、3台の機械を用いて2種類の製品X、Yの生産が可能である。下表には、製品を1単位生産するのに必要な各機械の工数と製品を1単位生産して得られる単位利益、および現状で使用可能な各機械の工数が示されている。
また、下図は、下表に示した各機械における使用可能工数の制約を図示したものである。
総利益が最も高くなる方策として、最も適切なものを下記の解答群から選べ。
〔解答群〕
ア
機械Aの使用可能工数を現状から4引き上げて6とする。
イ
機械Bの使用可能工数を現状から4引き上げて12とする。
ウ
機械Cの使用可能工数を現状から4引き上げて16とする。
エ
機械Bの使用可能工数を現状から2引き上げて10、機械Cの使用可能工数を現状から2引き上げて14とする。
出典: 中小企業診断協会|2020年度 第1次試験問題|運営管理(PDF)
解答
- 正解:イ
(機械Bの使用可能工数を8から4引き上げて12とする)
解説
1. 現状の制約条件と目的関数
- 目的関数(総利益):
Z = 3X + 5Y
(X:製品Xの生産量、Y:製品Yの生産量) - 制約条件(工数):
- 機械A: X ≤ 2
- 機械B: 2Y ≤ 8 → Y ≤ 4
- 機械C: 4X + 2Y ≤ 12
2. 現状の最適解と利益
- 実行可能領域の頂点候補:
- P:(2, 2) → Z = 16
- R:(0, 4) → Z = 20
- S:(1, 4) → Z = 23 ← 現状の最適解
- S点は、機械Bと機械Cの制約をギリギリ満たしており、これらがボトルネック。
3. 各選択肢の評価
| 選択肢 | 緩和内容 | 新たな最適点 | 総利益 | 増加幅 |
|---|---|---|---|---|
| ア | 機械Aを6に | X制約緩和 → 影響なし | 23 | ±0 |
| イ | 機械Bを12に | Y制約緩和 → (0, 6) | 30 | +7 |
| ウ | 機械Cを16に | C制約緩和 → (2, 4) | 26 | +3 |
| エ | B→10, C→14 | (1, 5) | 28 | +5 |
- 最も利益が増加するのは「イ」(機械Bの工数を12に引き上げた場合)
学習のポイント
シャドウ・プライスの考え方
- 制約が厳しい(=資源が不足している)ほど、その資源の価値は高い。
- 現状の最適点で目いっぱい使われている機械BとCが「価値の高い資源」。
- 特に機械Bは製品Y(利益5)にしか使われないため、Bの緩和は利益増に直結。
線形計画法の戦略
- 最適解は「実行可能領域の頂点」にある。
- 制約を緩和すると、実行可能領域が広がり、より高い利益点に移動できる。
- 単位利益の高い製品の生産を制限している制約を緩和するのが最も効果的。
