難易度・正答率・重要度
- 難易度: ★★☆☆☆(供給曲線と余剰の面積)
- 正答率: ★★★★☆(図の読み取り)
- 重要度: ★★★☆☆(生産者余剰・費用の基本)
問題文
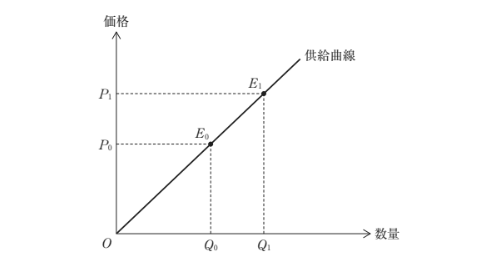
下図には、供給曲線が描かれている。この図に関する記述の正誤の組み合わせとして、最も適切なものを下記の解答群から選べ。
a
生産量が拡大するにつれて、限界費用は増加する。
b
価格が P0 のとき、生産者が必要最低限回収しなければならない費用の合計は三角形 OE0Q0 で示される。
c
価格が P1 のときの生産者余剰は、台形 P1E1E0P0 で示される。
〔解答群〕
ア
a:正 b:正 c:正
イ
a:正 b:正 c:誤
ウ
a:正 b:誤 c:誤
エ
a:誤 b:正 c:誤
オ
a:誤 b:誤 c:正
出典:中小企業診断協会|2022年度 第1次試験問題|経済学・経営政策(PDF)
解答
- 正解:イ(a:〇/b:〇/c:×)
解説
- a:〇
上に凸の右上がりの供給曲線は、産出量の増加に伴い限界費用が上昇することを表す。E₀(P₀, Q₀)からE₁(P₁, Q₁)へ移るほど、追加1単位の費用(限界費用)は高くなる。 - b:〇
価格がP₀のとき、0からQ₀までの必要最低限回収すべき費用(総可変費用)は「限界費用の積分=供給曲線下の面積」。図では原点OからE₀、Q₀で囲まれる三角形OE₀Q₀に一致する。 - c:×
価格がP₁での生産者余剰は「価格線P₁と供給曲線の間の面積(0~Q₁)」で定義される。台形P₁E₁E₀P₀はP₀水準の部分を含み、P₁時点の余剰範囲を越えているため不適切。正しくは「長方形OP₁Q₁から供給曲線下の三角形OE₁Q₁を差し引いた領域」。
学習のポイント
- 総可変費用: 供給曲線(限界費用)下の0~Qの面積。
- 生産者余剰: 価格×数量の長方形から、供給曲線下の面積(総可変費用)を差し引いた部分。
- 直観: 生産量が増えるほど追加生産の費用は高くなり、供給曲線は右上がりになる。
