難易度・正答率・重要度
- 難易度: ★★☆☆☆(等費用線・等産出曲線の関係)
- 正答率: ★★★★☆(典型図の読み取り)
- 重要度: ★★★☆☆(生産要素の最適選択)
問題文
下図は、労働と資本の価格および生産技術水準が一定で、かつ完全競争市場の下で2つの等費用線と等産出量曲線を示している。
この図に関する記述の正誤の組み合わせとして、最も適切なものを下記の解答群から選べ。
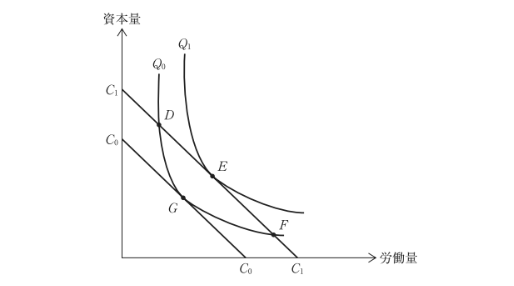
a
点Eは点Dと比べて、産出量は同じであるが、総要素費用はより少ない。
b
点Gは点Dと比べて、技術的限界代替率は同じであるが、産出量はより少ない。
c
総要素費用を一定とした場合、点Fでは、労働量を減らし資本量を増やすことで利潤を多くできる。
d
産出量を一定とした場合、点Dでは、資本量を減らし労働量を増やすことで最適生産を達成できる。
〔解答群〕
ア
a:正 b:正 c:正 d:誤
イ
a:正 b:誤 c:誤 d:正
ウ
a:誤 b:正 c:正 d:正
エ
a:誤 b:正 c:誤 d:誤
オ
a:誤 b:誤 c:正 d:正
出典: 中小企業診断協会|2024年度 第1次試験問題|経済学・経営政策(PDF)
解答
- 正解: オ(a:誤/b:誤/c:正/d:正)
解説
- a:×
同じ産出量(同一等産出曲線)で総費用がより少ない点は、等費用線が原点側(より低い費用)の線上にある必要がある。図の関係からEはDより費用が小さいとはいえず、記述は誤り。 - b:×
技術的限界代替率(MRTS)は等産出曲線の接線傾きで決まる。DとGが異なる位置ならMRTSが同じとは限らず、かつGがより低い産出量の等産出曲線上にあるため、記述は誤り。 - c:〇
総費用一定(同一等費用線)でFが等産出曲線の接点に達していない場合、労働を減らし資本を増やす(またはその逆)ことで、より高い等産出曲線へ到達し、産出が増え利潤が高まる。 - d:〇
産出量一定(同一等産出曲線)でDが費用最小の接点でなければ、資本を減らして労働を増やす(またはその逆)ことで、より低い等費用線に移り、同産出の費用を削減して最適化できる。
学習のポイント
- 最適生産の条件:
等産出曲線と等費用線が接する点(MRTS=要素価格比)が費用最小の組合せ。 - 費用一定・産出最大化:
等費用線上で、より外側の等産出曲線に届く組合せが望ましい。 - 産出一定・費用最小化:
同じ等産出曲線上で、できるだけ原点側の等費用線に移れる組合せが最適。 - MRTSの直感:
等産出曲線の接線の傾きが、労働と資本の限界代替の比率を示す。接点で要素価格比と一致する。
