難易度・正答率・重要度
- 難易度: ★★★☆☆(生産性の定義と計算)
- 正答率: ★★★☆☆(式の整理が鍵)
- 重要度: ★★★☆☆(人時生産性の実務応用)
問題文
下表は、4つの店舗における、ある期間の売上高、粗利高、従業員数、総作業時間をまとめたものである。各店舗で作業を効率化するためのシステムを導入し、1人当たりの作業時間を変えずに従業員を1人ずつ減らした場合、売上高と粗利高が変わらないとすると、システム導入前と比べて人時生産性で最も改善額が大きい店舗を下記の解答群から選べ。なお、ここで人時生産性は粗利高で算出するものとする。
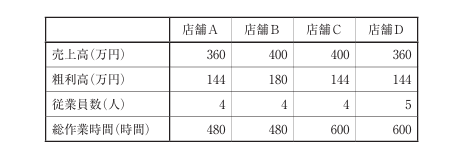
〔解答群〕
ア
店舗A
イ
店舗B
ウ
店舗C
エ
店舗D
出典: 中小企業診断協会|2024年度 第1次試験問題|運営管理(PDF)
解答
- 正解:イ(店舗B)
解説
- 前提の式整理:人時生産性の改善額
- 人時生産性(粗利ベース):粗利高 ÷ 総作業時間
- 従業員を1人減らす(1人当たり時間は同じ) ⇒ 新総時間=旧総時間×((1 – \frac{1}{従業員数}))
- 改善額=新生産性−旧生産性=(\frac{\text{粗利}}{H(1-\frac{1}{E})} – \frac{\text{粗利}}{H})
- 簡約すると、改善額=(\frac{\text{粗利}}{H} \cdot \frac{1}{E-1})
- 各店舗の改善額(万円/時間)
- 店舗A:(\frac{120}{480} \cdot \frac{1}{4-1} = 0.25 \cdot \frac{1}{3} \approx 0.0833)
- 店舗B:(\frac{90}{360} \cdot \frac{1}{3-1} = 0.25 \cdot \frac{1}{2} = 0.1250)
- 店舗C:(\frac{160}{600} \cdot \frac{1}{5-1} \approx 0.2667 \cdot 0.25 \approx 0.0667)
- 店舗D:(\frac{120}{480} \cdot \frac{1}{4-1} = 0.0833)
ア:×
改善額は店舗A約0.0833で最大ではない。
イ:〇
改善額は店舗Bが0.125で最大。
ウ:×
店舗Cは約0.0667で最小。
エ:×
店舗Dは約0.0833でAと同水準だが、Bより小さい。
学習のポイント
- 式の使い所: 従業員を1人減らす場合の新総時間は「旧総時間×(1−1/従業員数)」で一発。
- 改善額の一括比較: 改善額=(粗利/総時間)×1/(従業員数−1) を覚えると速い。
- 直観の補強: もともと人時粗利が高い店、従業員数が少ない店ほど改善幅が大きくなりやすい。
